In-Class Exercise 2A: Spatial Weights

Using sfdep package

Author

Goh Si Hui

Published

November 25, 2023

Modified

November 25, 2023

1 Task

For this task, we will be learning how to derive spatial weights using the sfdep package.

According to Josiah Parry, the developer of the package,

“sfdep builds on the great shoulders of spdep package for spatial dependence. sfdep creates an sf and tidyverse friendly interface to the package as well as introduces new functionality that is not present in spdep. sfdep utilizes list columns extensively to make this interface possible.”

2 Getting Started

We will first load the necessary packages using the following code chunk:

tmap: for thematic mapping
sf: for geospatial data handling (e.g. importing and exporting for spatial data and geoprocessing)
tidyverse: a family of R packages for non-spatial data handling
knitr: to generate static html tables
sfdep: to calculate spatial weights and matrices, space time cube and hot spot analysis

pacman::p_load(tmap, sf, tidyverse, sfdep, knitr)

3 Preparing the Geospatial Data

3.1 Importing the data

hunan <- st_read(dsn = "data/geospatial", layer="Hunan")

Reading layer `Hunan' from data source 
  `C:\sihuihui\ISSS624\In-class_Ex\In-class_Ex2\data\geospatial' 
  using driver `ESRI Shapefile'
Simple feature collection with 88 features and 7 fields
Geometry type: POLYGON
Dimension:     XY
Bounding box:  xmin: 108.7831 ymin: 24.6342 xmax: 114.2544 ymax: 30.12812
Geodetic CRS:  WGS 84

From the above outcome, we know that hunandata is simple feature (sf) data frame with 88 features (each representing 1 geographical entity), and each feature is a polygon.It uses the WGS84 projection.

4 Preparing the Aspatial Data

4.1 Importing the data

hunan2012 <- read.csv("data/aspatial/Hunan_2012.csv")

5 Combining Both Data Frames Using Left Join

hunan_GDPPC<- left_join(hunan, hunan2012) %>% 
                select(1:4, 7, 15)

When joining these 2 data frames, we did not specify the by= because there is a common column in both data frames (i.e., Country )

Other than joining both data frames, we also use select() to pick the relevant columns that we want. Note that the geometry column was retained even though it was not specified.

We typically use a left join with a spatial layer (e.g. hunan) and nonspatial layer (hunan_GDPPC) so that we can retain spatial geometric properties.

6 Plotting the choropleth Map

We use the following code to visualise the choropleth map of Hunan’s 2012 GDPPC.

tmap_mode("plot")
tm_shape(hunan_GDPPC) +
  tm_fill("GDPPC",
          style = "quantile",
          palette = "Blues",
          title = "GDPPC") + 
  tm_borders(alpha = 0.5) + 
  tm_layout(main.title = "Distribution of GDP per capita by district in Hunan (2012)", main.title.position="center",
            main.title.size = 1.2,
            legend.height = 0.45,
            legend.width = 0.35, 
            frame= TRUE) +
  tm_compass(type = "8star", size=2) +
  tm_scale_bar() +
  tm_grid(alpha = 0.2)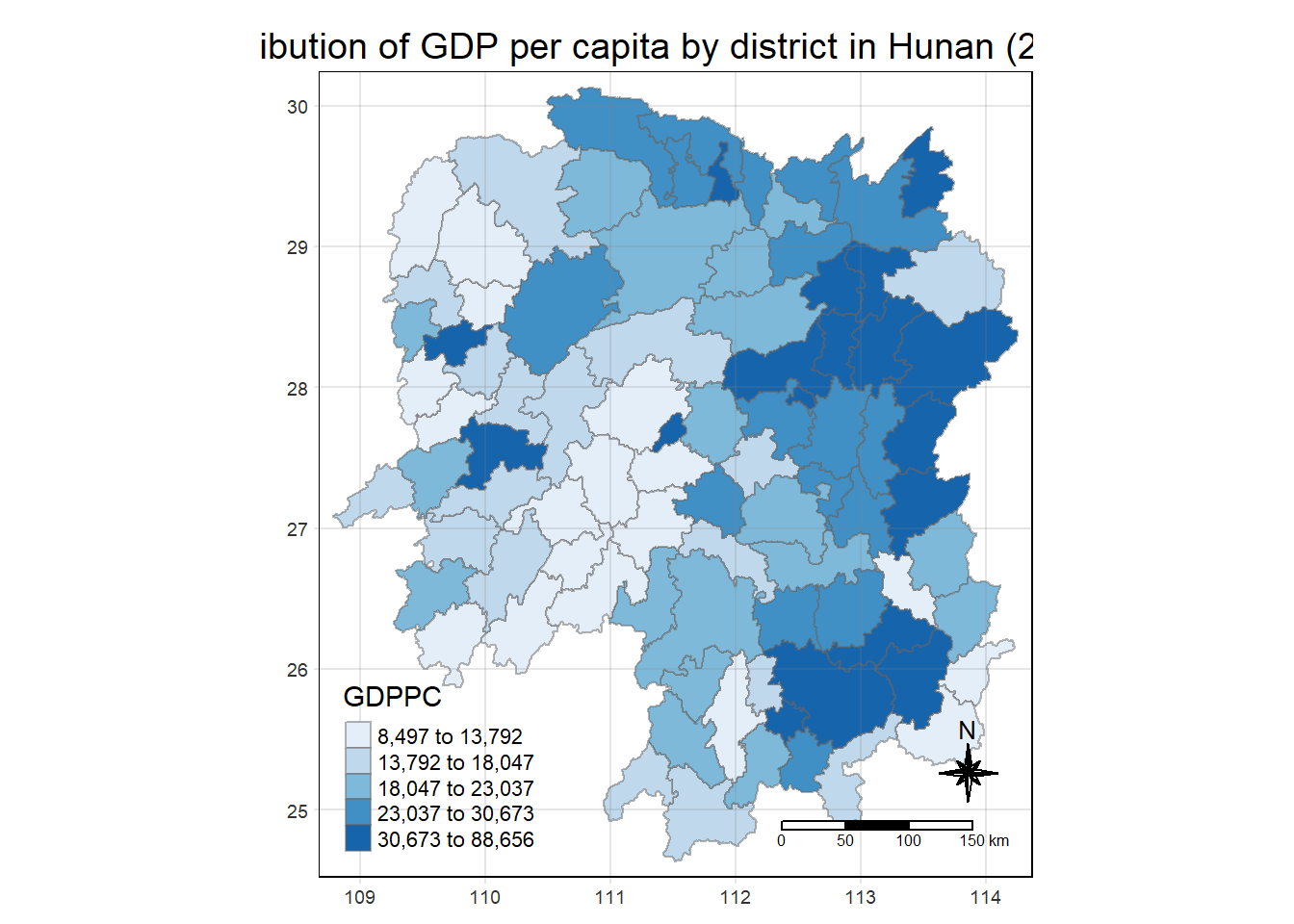

7 Defining Weight Matrix

As learnt in our hands-on exercises, we can define weight matrices based on contiguity (adjacency) or distance.

7.1 Contiguity Weight Matrix

To compute contiguity weight matrix using sfdep package, we perform the following steps:

identify contiguity neighbour list using st_contiguity() of sfdep package, and
derive the contiguity spatial weights using st_weights() of sfdep package.

To identify the contiguity neighbour list using Queen and Rook method, we use the following code chunks.

Queen
Rook

nb_queen <- hunan_GDPPC %>% 
  mutate(nb=st_contiguity(geometry),
         .before=1)

nb_rook <- hunan_GDPPC %>% 
  mutate(nb=st_contiguity(geometry, queen=FALSE),
         .before=1)

Let us take a look at the summary of the first lag neighbour list (i.e. nb) using the following code chunks.

Queen
Rook

summary(nb_queen$nb)

Neighbour list object:
Number of regions: 88 
Number of nonzero links: 448 
Percentage nonzero weights: 5.785124 
Average number of links: 5.090909 
Link number distribution:

 1  2  3  4  5  6  7  8  9 11 
 2  2 12 16 24 14 11  4  2  1 
2 least connected regions:
30 65 with 1 link
1 most connected region:
85 with 11 links

summary(nb_rook$nb)

Neighbour list object:
Number of regions: 88 
Number of nonzero links: 440 
Percentage nonzero weights: 5.681818 
Average number of links: 5 
Link number distribution:

 1  2  3  4  5  6  7  8  9 10 
 2  2 12 20 21 14 11  3  2  1 
2 least connected regions:
30 65 with 1 link
1 most connected region:
85 with 10 links

The summary report for Queen Contiguity based weight matrix shows that there are 88 area units in Hunan province. The most connected area unit has 11 neighbours. There are two are units with only one neighbour.

The summary report for Rook Contiguity based weight matrix shows that there are 88 area units in Hunan province. The most connected area unit has 10 neighbours. There are two are units with only one neighbour.

We can also display the output data frame using the following Methods. For the codes below, we will use nb_queen as example.

Option 1 - using the dataframe itself
Option 2 - Using kable() and head()

nb_queen

Simple feature collection with 88 features and 7 fields
Geometry type: POLYGON
Dimension:     XY
Bounding box:  xmin: 108.7831 ymin: 24.6342 xmax: 114.2544 ymax: 30.12812
Geodetic CRS:  WGS 84
First 10 features:
                               nb   NAME_2  ID_3    NAME_3   ENGTYPE_3
1                 2, 3, 4, 57, 85  Changde 21098   Anxiang      County
2               1, 57, 58, 78, 85  Changde 21100   Hanshou      County
3                     1, 4, 5, 85  Changde 21101    Jinshi County City
4                      1, 3, 5, 6  Changde 21102        Li      County
5                     3, 4, 6, 85  Changde 21103     Linli      County
6                4, 5, 69, 75, 85  Changde 21104    Shimen      County
7                  67, 71, 74, 84 Changsha 21109   Liuyang County City
8       9, 46, 47, 56, 78, 80, 86 Changsha 21110 Ningxiang      County
9           8, 66, 68, 78, 84, 86 Changsha 21111 Wangcheng      County
10 16, 17, 19, 20, 22, 70, 72, 73 Chenzhou 21112     Anren      County
      County GDPPC                       geometry
1    Anxiang 23667 POLYGON ((112.0625 29.75523...
2    Hanshou 20981 POLYGON ((112.2288 29.11684...
3     Jinshi 34592 POLYGON ((111.8927 29.6013,...
4         Li 24473 POLYGON ((111.3731 29.94649...
5      Linli 25554 POLYGON ((111.6324 29.76288...
6     Shimen 27137 POLYGON ((110.8825 30.11675...
7    Liuyang 63118 POLYGON ((113.9905 28.5682,...
8  Ningxiang 62202 POLYGON ((112.7181 28.38299...
9  Wangcheng 70666 POLYGON ((112.7914 28.52688...
10     Anren 12761 POLYGON ((113.1757 26.82734...

kable(head(nb_queen, n=10))

nb	NAME_2	ID_3	NAME_3	ENGTYPE_3	County	GDPPC	geometry
2, 3, 4, 57, 85	Changde	21098	Anxiang	County	Anxiang	23667	POLYGON ((112.0625 29.75523…
1, 57, 58, 78, 85	Changde	21100	Hanshou	County	Hanshou	20981	POLYGON ((112.2288 29.11684…
1, 4, 5, 85	Changde	21101	Jinshi	County City	Jinshi	34592	POLYGON ((111.8927 29.6013,…
1, 3, 5, 6	Changde	21102	Li	County	Li	24473	POLYGON ((111.3731 29.94649…
3, 4, 6, 85	Changde	21103	Linli	County	Linli	25554	POLYGON ((111.6324 29.76288…
4, 5, 69, 75, 85	Changde	21104	Shimen	County	Shimen	27137	POLYGON ((110.8825 30.11675…
67, 71, 74, 84	Changsha	21109	Liuyang	County City	Liuyang	63118	POLYGON ((113.9905 28.5682,…
9, 46, 47, 56, 78, 80, 86	Changsha	21110	Ningxiang	County	Ningxiang	62202	POLYGON ((112.7181 28.38299…
8, 66, 68, 78, 84, 86	Changsha	21111	Wangcheng	County	Wangcheng	70666	POLYGON ((112.7914 28.52688…
16, 17, 19, 20, 22, 70, 72, 73	Chenzhou	21112	Anren	County	Anren	12761	POLYGON ((113.1757 26.82734…

7.1.1 Identifying higher Order Neighbours

In class, we learnt that other than the immediate neighbours (i.e. those regions along the boundaries of an area), we can also find out their neighbour’s neigbours (i.e., higher order contiguity neighbours). We can do this using st_nb_lag_cumul() of sfdep package.This function Creates an encompassing neighbor list of the order specified. For example, if the order is 2 the result contains both 1st and 2nd order neighbors.

In the following code chunk, we will generate the 1st and 2nd order neighbours for each region in Hunan.

nb2_queen <- hunan_GDPPC %>% 
  mutate(nb = st_contiguity(geometry), 
         nb2 = st_nb_lag_cumul(nb,2),
         .before = 1)

Let’s take a look at the differences between 1st order only and output with both 1st and 2nd order neighhbours

1st Order Only
1st and 2nd Order

nb <- st_contiguity(sf::st_geometry(hunan_GDPPC))
summary(nb)

Neighbour list object:
Number of regions: 88 
Number of nonzero links: 448 
Percentage nonzero weights: 5.785124 
Average number of links: 5.090909 
Link number distribution:

 1  2  3  4  5  6  7  8  9 11 
 2  2 12 16 24 14 11  4  2  1 
2 least connected regions:
30 65 with 1 link
1 most connected region:
85 with 11 links

summary(nb2_queen)

Neighbour list object:
Number of regions: 88 
Number of nonzero links: 448 
Percentage nonzero weights: 5.785124 
Average number of links: 5.090909 
Link number distribution:

 1  2  3  4  5  6  7  8  9 11 
 2  2 12 16 24 14 11  4  2  1 
2 least connected regions:
30 65 with 1 link
1 most connected region:
85 with 11 links
Neighbour list object:
Number of regions: 88 
Number of nonzero links: 1324 
Percentage nonzero weights: 17.09711 
Average number of links: 15.04545 
Link number distribution:

 5  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 26 28 33 
 2  1  6  4  5  4  8  5 10  4  4  8  4  8  5  2  2  1  2  1  1  1 
2 least connected regions:
30 88 with 5 links
1 most connected region:
56 with 33 links

    nb         nb2          NAME_2               ID_3          NAME_3         
 NULL:NULL   NULL:NULL   Length:88          Min.   :21098   Length:88         
                         Class :character   1st Qu.:21125   Class :character  
                         Mode  :character   Median :21150   Mode  :character  
                                            Mean   :21150                     
                                            3rd Qu.:21174                     
                                            Max.   :21201                     
  ENGTYPE_3            County              GDPPC                geometry 
 Length:88          Length:88          Min.   : 8497   POLYGON      :88  
 Class :character   Class :character   1st Qu.:14566   epsg:4326    : 0  
 Mode  :character   Mode  :character   Median :20433   +proj=long...: 0  
                                       Mean   :24405                     
                                       3rd Qu.:27224                     
                                       Max.   :88656

When higher order neighbours are included, we note that the number of nonzero links and the average number of links increased.

7.2 Distance- based Weight Matrix

There are three popularly used distance-based spatial weights, they are:

fixed distance weights,
adaptive distance weights, and
inverse distance weights (IDW).

7.2.1 Fixed Distance weights

We will use the following code chunk to determine the upper limit for distance band. This will be needed for the subsequent computation of fixed distance weight matrix.

geo <- sf::st_geometry(hunan_GDPPC)
nb <- st_knn(geo, longlat=TRUE)
dists <- unlist(st_nb_dists(geo, nb))

Explanation of the functions used above

st_geometry(): Get, set, replace or rename geometry from an sf object
st_knn(): Identifies the k nearest neighbors for given point geometry
st_nb_dists():From an nb list and point geometry, return a list of distances for each observation’s neighbors list.
unlist(): Given a list structure, simplifies it to produce a vector which contains all the atomic components which occur in the list.

We will derive the summary statistics of the nearest neighbour distances vector (i.e., dists) using the following code chunk.

summary(dists)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  21.56   29.11   36.89   37.34   43.21   65.80

The summary statistics report above shows that the maximum nearest neighbour distance is 65.80km. By using a threshold value of 66km will ensure that each area will have at least one neighbour.

Now we will go ahead to compute the fixed distance weights by using the code chunk below.

wm_fd <- hunan_GDPPC %>%
  mutate(nb=st_dist_band(geometry, upper=66),
         wt = st_weights(nb), 
         .before = 1)

Explanation of the functions used above

st_dist_band: To identify neighbours based on a distance band (i.e., 66km). The output is a list of neighbours (i.e., nb).
st_weights: To calcualte polygon spatial weights of the nb list. Note that:
- the default style argument is set to “W” for row standardised weights, and
- the default allow_zero is set to TRUE, assigns zero as lagged value to zone without neighbours.

Let’s take a look at the data frame.

wm_fd

Simple feature collection with 88 features and 8 fields
Geometry type: POLYGON
Dimension:     XY
Bounding box:  xmin: 108.7831 ymin: 24.6342 xmax: 114.2544 ymax: 30.12812
Geodetic CRS:  WGS 84
First 10 features:
                       nb
1      2, 3, 4, 5, 57, 64
2       1, 57, 58, 78, 85
3             1, 4, 5, 57
4              1, 3, 5, 6
5          1, 3, 4, 6, 69
6                4, 5, 69
7              67, 71, 84
8       9, 46, 47, 78, 80
9   8, 46, 66, 68, 84, 86
10 16, 20, 22, 70, 72, 73
                                                                 wt   NAME_2
1  0.1666667, 0.1666667, 0.1666667, 0.1666667, 0.1666667, 0.1666667  Changde
2                                           0.2, 0.2, 0.2, 0.2, 0.2  Changde
3                                            0.25, 0.25, 0.25, 0.25  Changde
4                                            0.25, 0.25, 0.25, 0.25  Changde
5                                           0.2, 0.2, 0.2, 0.2, 0.2  Changde
6                                   0.3333333, 0.3333333, 0.3333333  Changde
7                                   0.3333333, 0.3333333, 0.3333333 Changsha
8                                           0.2, 0.2, 0.2, 0.2, 0.2 Changsha
9  0.1666667, 0.1666667, 0.1666667, 0.1666667, 0.1666667, 0.1666667 Changsha
10 0.1666667, 0.1666667, 0.1666667, 0.1666667, 0.1666667, 0.1666667 Chenzhou
    ID_3    NAME_3   ENGTYPE_3    County GDPPC                       geometry
1  21098   Anxiang      County   Anxiang 23667 POLYGON ((112.0625 29.75523...
2  21100   Hanshou      County   Hanshou 20981 POLYGON ((112.2288 29.11684...
3  21101    Jinshi County City    Jinshi 34592 POLYGON ((111.8927 29.6013,...
4  21102        Li      County        Li 24473 POLYGON ((111.3731 29.94649...
5  21103     Linli      County     Linli 25554 POLYGON ((111.6324 29.76288...
6  21104    Shimen      County    Shimen 27137 POLYGON ((110.8825 30.11675...
7  21109   Liuyang County City   Liuyang 63118 POLYGON ((113.9905 28.5682,...
8  21110 Ningxiang      County Ningxiang 62202 POLYGON ((112.7181 28.38299...
9  21111 Wangcheng      County Wangcheng 70666 POLYGON ((112.7914 28.52688...
10 21112     Anren      County     Anren 12761 POLYGON ((113.1757 26.82734...

7.2.2 Adaptive Distance weights

We will derive adaptive spatial weights using the following code chunk.

wm_ad <- hunan_GDPPC %>% 
  mutate(nb = st_knn(geometry, 
         k = 8),
         wt = st_weights(nb),
         .before = 1)

Explanation of the functions used above

st_knn(): To identify neighbours based on a k (i.e., k=8 indicates the nearest 8 neighbours). The output is a list of neighbours (i.e., nb).

7.2.3 Inverse Distance weights

We will derive an inverse distance weights using the following code chunk.

wm_idw <- hunan_GDPPC %>%
  mutate(nb = st_contiguity(geometry), 
         wt = st_inverse_distance(nb, geometry, 
                                  scale = 1,
                                  alpha = 1),
         .before=1)

Explanation of the function used above

st_inverse_distance(): To calculate inverse distance weights of neighbours on the nb list.