Hands-on Exercise 1A: Geospatial Data Wrangling with R

Author

Goh Si Hui

Published

November 16, 2023

Modified

November 18, 2023

1 Overview

In this hands-on exercise, I will be sharing how to import and wrangle geospatial data using appropriate R packages.

2 Getting Started

2.1 Packages

For this exercise, we will be using sf and tidyverse packages. The code chunk below installs and loads sf and tidyverse packages into R environment.

pacman::p_load(sf, tidyverse)

2.2 Data Acquisition and Extraction

We will extract the following data sets from these sources:

Master Plan 2014 Subzone Boundary (Web) from data.gov.sg
Pre-Schools Location from data.gov.sg
Cycling Path from LTADataMall
Latest version of Singapore Airbnb listing data from Inside Airbnb

After we have downloaded these data sets, we created a sub-folder called data. Within the datasub-folder, we created 2 sub-folders, namely geospatial and aspatial. Master Plan 2014 Subzone Boundary (Web), Pre-Schools Location and Cycling Path files should be placed in the geospatial folder while the Singapore Airbnb listing data should be in the aspatial folder.

3 Importing Geospatial Data

3.1 Importing polygon feature data

The code chunk below uses st_read() function of sf package to import the planning subzones, which is a polygon feature data frame.

mpsz <- st_read(dsn = "data/geospatial", layer = "MP14_SUBZONE_WEB_PL")

Reading layer `MP14_SUBZONE_WEB_PL' from data source 
  `C:\sihuihui\ISSS624\Hands-on_Ex\Hands-on_Ex1\data\geospatial' 
  using driver `ESRI Shapefile'
Simple feature collection with 323 features and 15 fields
Geometry type: MULTIPOLYGON
Dimension:     XY
Bounding box:  xmin: 2667.538 ymin: 15748.72 xmax: 56396.44 ymax: 50256.33
Projected CRS: SVY21

The message above also tells us that mpsz’s geometry type is multipolygon, there are a total of 323 multipolygon features and 15 fields in mpsz and it is in svy21 projected coordinates systems.

3.2 Importing polyline feature data in shapefile form

The code chunk below uses st_read() function of sf package to import CyclingPath shape file into R as line feature data frame.

cyclingpath = st_read(dsn = "data/geospatial", layer = "CyclingPathGazette")

Reading layer `CyclingPathGazette' from data source 
  `C:\sihuihui\ISSS624\Hands-on_Ex\Hands-on_Ex1\data\geospatial' 
  using driver `ESRI Shapefile'
Simple feature collection with 2558 features and 2 fields
Geometry type: MULTILINESTRING
Dimension:     XY
Bounding box:  xmin: 11854.32 ymin: 28347.98 xmax: 42626.09 ymax: 48948.15
Projected CRS: SVY21

From the above, we know that cyclingpath has a total of 2558 features and 2 fields, is a multilinestring, and is in svy21 projected coordinates system.

3.3 Importing GIS data in kml format

We will also use st_read() to import GIS data in kml format:

preschool = st_read("data/geospatial/PreSchoolsLocation.kml")

Reading layer `PRESCHOOLS_LOCATION' from data source 
  `C:\sihuihui\ISSS624\Hands-on_Ex\Hands-on_Ex1\data\geospatial\PreSchoolsLocation.kml' 
  using driver `KML'
Simple feature collection with 2290 features and 2 fields
Geometry type: POINT
Dimension:     XYZ
Bounding box:  xmin: 103.6878 ymin: 1.247759 xmax: 103.9897 ymax: 1.462134
z_range:       zmin: 0 zmax: 0
Geodetic CRS:  WGS 84

From the above, we know that preschool has 2290 features and 2 fields, a point feature data frame, and is in wgs84 coordinates system.

4 Checking the Content of A Simple Feature Data Frame

We can use different ways to retrieve information related to the content of a simple feature data frame.

4.1 Working with st_geometry()

st_geometry() displays basic information of the feature class such as type of geometry, the geographic extent of the features and the coordinate system of the data.

st_geometry(mpsz)

Geometry set for 323 features 
Geometry type: MULTIPOLYGON
Dimension:     XY
Bounding box:  xmin: 2667.538 ymin: 15748.72 xmax: 56396.44 ymax: 50256.33
Projected CRS: SVY21
First 5 geometries:

4.2 Working with glimpse()

glimpse() reveals the data type of each fields.

glimpse(mpsz)

Rows: 323
Columns: 16
$ OBJECTID   <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, …
$ SUBZONE_NO <int> 1, 1, 3, 8, 3, 7, 9, 2, 13, 7, 12, 6, 1, 5, 1, 1, 3, 2, 2, …
$ SUBZONE_N  <chr> "MARINA SOUTH", "PEARL'S HILL", "BOAT QUAY", "HENDERSON HIL…
$ SUBZONE_C  <chr> "MSSZ01", "OTSZ01", "SRSZ03", "BMSZ08", "BMSZ03", "BMSZ07",…
$ CA_IND     <chr> "Y", "Y", "Y", "N", "N", "N", "N", "Y", "N", "N", "N", "N",…
$ PLN_AREA_N <chr> "MARINA SOUTH", "OUTRAM", "SINGAPORE RIVER", "BUKIT MERAH",…
$ PLN_AREA_C <chr> "MS", "OT", "SR", "BM", "BM", "BM", "BM", "SR", "QT", "QT",…
$ REGION_N   <chr> "CENTRAL REGION", "CENTRAL REGION", "CENTRAL REGION", "CENT…
$ REGION_C   <chr> "CR", "CR", "CR", "CR", "CR", "CR", "CR", "CR", "CR", "CR",…
$ INC_CRC    <chr> "5ED7EB253F99252E", "8C7149B9EB32EEFC", "C35FEFF02B13E0E5",…
$ FMEL_UPD_D <date> 2014-12-05, 2014-12-05, 2014-12-05, 2014-12-05, 2014-12-05…
$ X_ADDR     <dbl> 31595.84, 28679.06, 29654.96, 26782.83, 26201.96, 25358.82,…
$ Y_ADDR     <dbl> 29220.19, 29782.05, 29974.66, 29933.77, 30005.70, 29991.38,…
$ SHAPE_Leng <dbl> 5267.381, 3506.107, 1740.926, 3313.625, 2825.594, 4428.913,…
$ SHAPE_Area <dbl> 1630379.27, 559816.25, 160807.50, 595428.89, 387429.44, 103…
$ geometry   <MULTIPOLYGON [m]> MULTIPOLYGON (((31495.56 30..., MULTIPOLYGON (…

4.3 Working with head()

While glimpse() displays all the variables in the feature object, head() reveals the complete information of a feature object, which gives us a snapshot of the simple feature data frame.

head(mpsz, n=5)

Simple feature collection with 5 features and 15 fields
Geometry type: MULTIPOLYGON
Dimension:     XY
Bounding box:  xmin: 25867.68 ymin: 28369.47 xmax: 32362.39 ymax: 30435.54
Projected CRS: SVY21
  OBJECTID SUBZONE_NO      SUBZONE_N SUBZONE_C CA_IND      PLN_AREA_N
1        1          1   MARINA SOUTH    MSSZ01      Y    MARINA SOUTH
2        2          1   PEARL'S HILL    OTSZ01      Y          OUTRAM
3        3          3      BOAT QUAY    SRSZ03      Y SINGAPORE RIVER
4        4          8 HENDERSON HILL    BMSZ08      N     BUKIT MERAH
5        5          3        REDHILL    BMSZ03      N     BUKIT MERAH
  PLN_AREA_C       REGION_N REGION_C          INC_CRC FMEL_UPD_D   X_ADDR
1         MS CENTRAL REGION       CR 5ED7EB253F99252E 2014-12-05 31595.84
2         OT CENTRAL REGION       CR 8C7149B9EB32EEFC 2014-12-05 28679.06
3         SR CENTRAL REGION       CR C35FEFF02B13E0E5 2014-12-05 29654.96
4         BM CENTRAL REGION       CR 3775D82C5DDBEFBD 2014-12-05 26782.83
5         BM CENTRAL REGION       CR 85D9ABEF0A40678F 2014-12-05 26201.96
    Y_ADDR SHAPE_Leng SHAPE_Area                       geometry
1 29220.19   5267.381  1630379.3 MULTIPOLYGON (((31495.56 30...
2 29782.05   3506.107   559816.2 MULTIPOLYGON (((29092.28 30...
3 29974.66   1740.926   160807.5 MULTIPOLYGON (((29932.33 29...
4 29933.77   3313.625   595428.9 MULTIPOLYGON (((27131.28 30...
5 30005.70   2825.594   387429.4 MULTIPOLYGON (((26451.03 30...

Interesting info found!

Here is an article on the difference between glimpse() and head().

“the head() function shows the first few rows (observations) of the Data Frame. The glimpse() function displays the number of observations, and variables (columns) along with the type, name, and values of the latter.”

5 Plotting Geospatial Data

Other than looking at feature information, we should also visualise geospatial features. plot() is a quick and useful way to plot geospatial features:

plot(mpsz)

plot() returns us a multi-plot of all attributes, up to a reasonable maximum as shown above.

Note

If plot() is unable to plot all attributes, a warning would appear.

We can choose to plot only the geometry using the code chunk below.

plot(st_geometry(mpsz))

Alternatively, we can also choose the plot the sf object by using a specific attribute as shown in the code chunk below.

plot(mpsz["PLN_AREA_N"])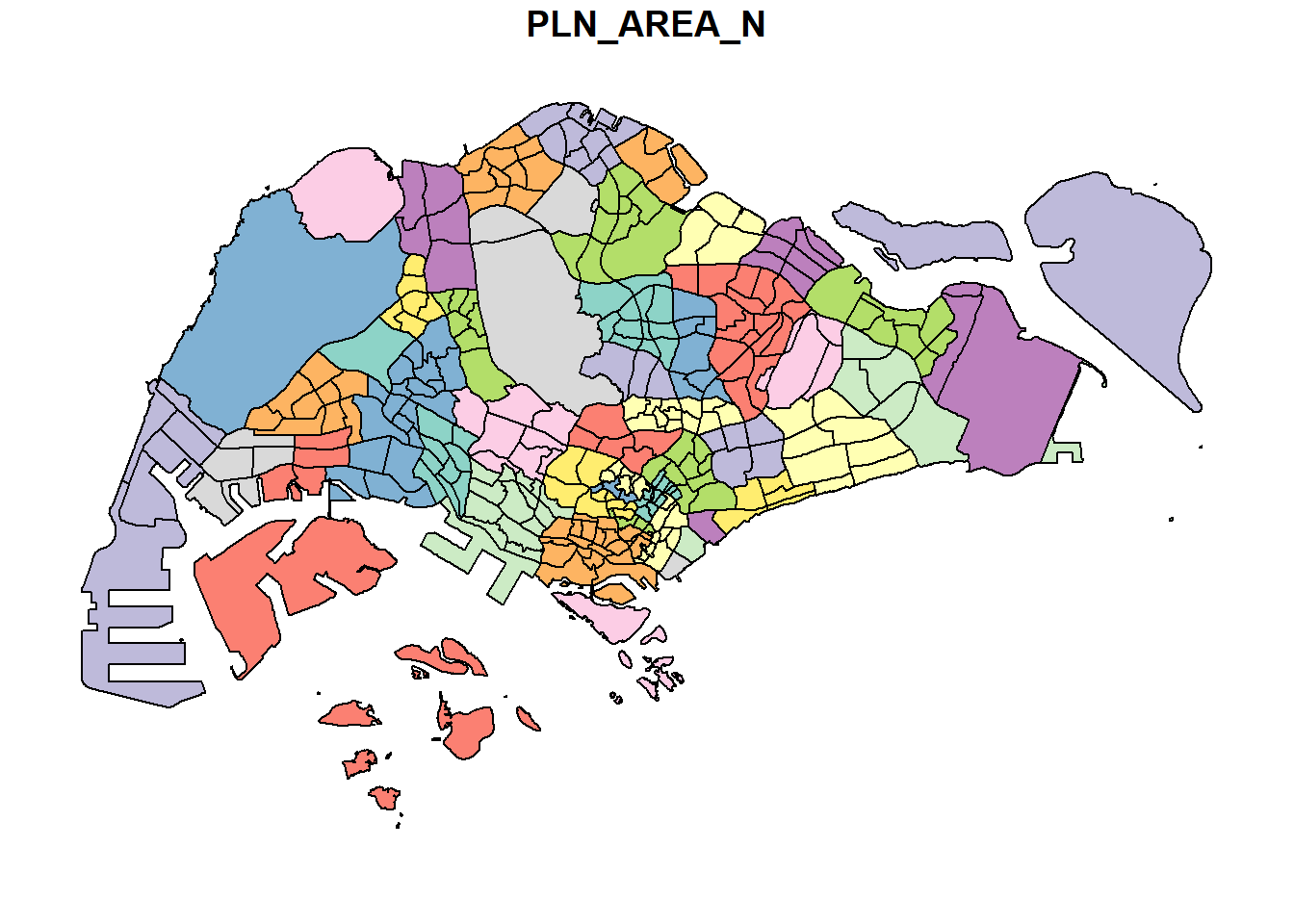

Note

We will learn more about plotting high cartographic quality plots using tmap package in Hands-On Exercise 1B.

6 Working with MAP Projection

Map projection is an important property of a geospatial data. In order to perform geoprocessing using two geospatial data, we need to ensure that both geospatial data are projected using similar coordinate system. In this section, we will project a simple feature data frame from one coordinate sstem to another coordinate system.

Note

You can read more about map projections in general here and Singapore’s map projections here.

6.1 Assigning EPSG code to a simple feature data frame

First, we will check the coordinate system of mpsz simple feature data frame using st_crs() of sf package:

st_crs(mpsz)

Coordinate Reference System:
  User input: SVY21 
  wkt:
PROJCRS["SVY21",
    BASEGEOGCRS["SVY21[WGS84]",
        DATUM["World Geodetic System 1984",
            ELLIPSOID["WGS 84",6378137,298.257223563,
                LENGTHUNIT["metre",1]],
            ID["EPSG",6326]],
        PRIMEM["Greenwich",0,
            ANGLEUNIT["Degree",0.0174532925199433]]],
    CONVERSION["unnamed",
        METHOD["Transverse Mercator",
            ID["EPSG",9807]],
        PARAMETER["Latitude of natural origin",1.36666666666667,
            ANGLEUNIT["Degree",0.0174532925199433],
            ID["EPSG",8801]],
        PARAMETER["Longitude of natural origin",103.833333333333,
            ANGLEUNIT["Degree",0.0174532925199433],
            ID["EPSG",8802]],
        PARAMETER["Scale factor at natural origin",1,
            SCALEUNIT["unity",1],
            ID["EPSG",8805]],
        PARAMETER["False easting",28001.642,
            LENGTHUNIT["metre",1],
            ID["EPSG",8806]],
        PARAMETER["False northing",38744.572,
            LENGTHUNIT["metre",1],
            ID["EPSG",8807]]],
    CS[Cartesian,2],
        AXIS["(E)",east,
            ORDER[1],
            LENGTHUNIT["metre",1,
                ID["EPSG",9001]]],
        AXIS["(N)",north,
            ORDER[2],
            LENGTHUNIT["metre",1,
                ID["EPSG",9001]]]]

Although mpsz data frame is projected in svy21, the above results shows that the EPSG is 9001, which is the wrong EPSG code because the correct EPSG code for svy21 should be 3414.

Hence we will assign the correct EPSG code to mpsz data frame using st_set_crs() of sf package:

mpsz3414 <- st_set_crs(mpsz, 3414)

We will check the coordinate system of mpsz simple feature data frame using st_crs() and we should see that the EPSG code is now 3414.

st_crs(mpsz3414)

Coordinate Reference System:
  User input: EPSG:3414 
  wkt:
PROJCRS["SVY21 / Singapore TM",
    BASEGEOGCRS["SVY21",
        DATUM["SVY21",
            ELLIPSOID["WGS 84",6378137,298.257223563,
                LENGTHUNIT["metre",1]]],
        PRIMEM["Greenwich",0,
            ANGLEUNIT["degree",0.0174532925199433]],
        ID["EPSG",4757]],
    CONVERSION["Singapore Transverse Mercator",
        METHOD["Transverse Mercator",
            ID["EPSG",9807]],
        PARAMETER["Latitude of natural origin",1.36666666666667,
            ANGLEUNIT["degree",0.0174532925199433],
            ID["EPSG",8801]],
        PARAMETER["Longitude of natural origin",103.833333333333,
            ANGLEUNIT["degree",0.0174532925199433],
            ID["EPSG",8802]],
        PARAMETER["Scale factor at natural origin",1,
            SCALEUNIT["unity",1],
            ID["EPSG",8805]],
        PARAMETER["False easting",28001.642,
            LENGTHUNIT["metre",1],
            ID["EPSG",8806]],
        PARAMETER["False northing",38744.572,
            LENGTHUNIT["metre",1],
            ID["EPSG",8807]]],
    CS[Cartesian,2],
        AXIS["northing (N)",north,
            ORDER[1],
            LENGTHUNIT["metre",1]],
        AXIS["easting (E)",east,
            ORDER[2],
            LENGTHUNIT["metre",1]],
    USAGE[
        SCOPE["Cadastre, engineering survey, topographic mapping."],
        AREA["Singapore - onshore and offshore."],
        BBOX[1.13,103.59,1.47,104.07]],
    ID["EPSG",3414]]

6.2 Transforming the projection of preschool from wgs84 to svy21

Using st_crs(), we check the projection of preschool data frame:

st_crs(preschool)

Coordinate Reference System:
  User input: WGS 84 
  wkt:
GEOGCRS["WGS 84",
    DATUM["World Geodetic System 1984",
        ELLIPSOID["WGS 84",6378137,298.257223563,
            LENGTHUNIT["metre",1]]],
    PRIMEM["Greenwich",0,
        ANGLEUNIT["degree",0.0174532925199433]],
    CS[ellipsoidal,2],
        AXIS["geodetic latitude (Lat)",north,
            ORDER[1],
            ANGLEUNIT["degree",0.0174532925199433]],
        AXIS["geodetic longitude (Lon)",east,
            ORDER[2],
            ANGLEUNIT["degree",0.0174532925199433]],
    ID["EPSG",4326]]

As preschool is in wgs84 coordinate system, we will need to reproject preschool from a wgs84 coordinate system to svy21 coordinate system using st_transform() .

Note

Note that st_transform() converts or transforms coordinates of simple feature while st_set_crs() change the coordinate reference system without modifying any coordinates.

preschool3414 <- st_transform(preschool, crs = 3414)

We will check the projection of preschool data frame:

st_crs(preschool3414)

Coordinate Reference System:
  User input: EPSG:3414 
  wkt:
PROJCRS["SVY21 / Singapore TM",
    BASEGEOGCRS["SVY21",
        DATUM["SVY21",
            ELLIPSOID["WGS 84",6378137,298.257223563,
                LENGTHUNIT["metre",1]]],
        PRIMEM["Greenwich",0,
            ANGLEUNIT["degree",0.0174532925199433]],
        ID["EPSG",4757]],
    CONVERSION["Singapore Transverse Mercator",
        METHOD["Transverse Mercator",
            ID["EPSG",9807]],
        PARAMETER["Latitude of natural origin",1.36666666666667,
            ANGLEUNIT["degree",0.0174532925199433],
            ID["EPSG",8801]],
        PARAMETER["Longitude of natural origin",103.833333333333,
            ANGLEUNIT["degree",0.0174532925199433],
            ID["EPSG",8802]],
        PARAMETER["Scale factor at natural origin",1,
            SCALEUNIT["unity",1],
            ID["EPSG",8805]],
        PARAMETER["False easting",28001.642,
            LENGTHUNIT["metre",1],
            ID["EPSG",8806]],
        PARAMETER["False northing",38744.572,
            LENGTHUNIT["metre",1],
            ID["EPSG",8807]]],
    CS[Cartesian,2],
        AXIS["northing (N)",north,
            ORDER[1],
            LENGTHUNIT["metre",1]],
        AXIS["easting (E)",east,
            ORDER[2],
            LENGTHUNIT["metre",1]],
    USAGE[
        SCOPE["Cadastre, engineering survey, topographic mapping."],
        AREA["Singapore - onshore and offshore."],
        BBOX[1.13,103.59,1.47,104.07]],
    ID["EPSG",3414]]

7 Importing and Converting an Aspatial Data

In this section, we will import an aspatial data into R environment and save it as a tibble data frame. Then, convert it into a simple feature data frame using the x- and y- coordinates in listing of Inside Airbnb data.

7.1 Importing the aspatial data

We use read_csv() of readr package to import the aspatial data in. The output is listings and it is a tibble data frame;

listings <- read_csv("data/aspatial/listings.csv")

We check the imported data using list() of Base R.

list(listings)

[[1]]
# A tibble: 3,483 × 18
       id name      host_id host_name neighbourhood_group neighbourhood latitude
    <dbl> <chr>       <dbl> <chr>     <chr>               <chr>            <dbl>
 1  71609 Villa in…  367042 Belinda   East Region         Tampines          1.35
 2  71896 Home in …  367042 Belinda   East Region         Tampines          1.35
 3  71903 Home in …  367042 Belinda   East Region         Tampines          1.35
 4 275343 Rental u… 1439258 Kay       Central Region      Bukit Merah       1.29
 5 275344 Rental u… 1439258 Kay       Central Region      Bukit Merah       1.29
 6 289234 Home in …  367042 Belinda   East Region         Tampines          1.34
 7 294281 Rental u… 1521514 Elizabeth Central Region      Newton            1.31
 8 324945 Rental u… 1439258 Kay       Central Region      Bukit Merah       1.29
 9 330095 Rental u… 1439258 Kay       Central Region      Bukit Merah       1.29
10 369141 Place to… 1521514 Elizabeth Central Region      Newton            1.31
# ℹ 3,473 more rows
# ℹ 11 more variables: longitude <dbl>, room_type <chr>, price <dbl>,
#   minimum_nights <dbl>, number_of_reviews <dbl>, last_review <date>,
#   reviews_per_month <dbl>, calculated_host_listings_count <dbl>,
#   availability_365 <dbl>, number_of_reviews_ltm <dbl>, license <chr>

The output reveals that listing tibble data frame consists of 4252 rows and 16 columns. We will be using the latitude and longitude from listings to create a simple feature data frame.

7.2 Creating a simple feature data frame from an aspatial data frame

The code chunk below converts listing data frame into a simple feature data frame by using st_as_sf() of sf packages.

listings_sf <- st_as_sf(listings, coords = c("longitude", "latitude"), crs=4326) %>%
  st_transform(crs = 3414)

We then use glimpse() to examine the content of the newly created simple feature data frame.

glimpse(listings_sf)

Rows: 3,483
Columns: 17
$ id                             <dbl> 71609, 71896, 71903, 275343, 275344, 28…
$ name                           <chr> "Villa in Singapore · ★4.44 · 2 bedroom…
$ host_id                        <dbl> 367042, 367042, 367042, 1439258, 143925…
$ host_name                      <chr> "Belinda", "Belinda", "Belinda", "Kay",…
$ neighbourhood_group            <chr> "East Region", "East Region", "East Reg…
$ neighbourhood                  <chr> "Tampines", "Tampines", "Tampines", "Bu…
$ room_type                      <chr> "Private room", "Private room", "Privat…
$ price                          <dbl> 150, 80, 80, 55, 69, 220, 85, 75, 45, 7…
$ minimum_nights                 <dbl> 92, 92, 92, 60, 60, 92, 92, 60, 60, 92,…
$ number_of_reviews              <dbl> 20, 24, 47, 22, 17, 12, 133, 18, 6, 81,…
$ last_review                    <date> 2020-01-17, 2019-10-13, 2020-01-09, 20…
$ reviews_per_month              <dbl> 0.14, 0.16, 0.31, 0.17, 0.12, 0.09, 0.9…
$ calculated_host_listings_count <dbl> 5, 5, 5, 52, 52, 5, 7, 52, 52, 7, 7, 1,…
$ availability_365               <dbl> 89, 89, 89, 275, 274, 89, 365, 365, 365…
$ number_of_reviews_ltm          <dbl> 0, 0, 0, 0, 3, 0, 0, 1, 3, 0, 0, 0, 0, …
$ license                        <chr> NA, NA, NA, "S0399", "S0399", NA, NA, "…
$ geometry                       <POINT [m]> POINT (41972.5 36390.05), POINT (…

Table above shows the content of listing_sf. Notice that a new column called geometry has been added into the data frame. On the other hand, the longitude and latitude columns have been dropped from the data frame.

8 Geoprocessing with sf package

In this section, we will learn to perform tow commonly used geoprocessing functions: buffering and point in polygon count.

8.1 Buffering

The scenario:

The authority is planning to upgrade the exiting cycling path. To do so, they need to acquire 5 metres of reserved land on the both sides of the current cycling path. You are tasked to determine the extend of the land need to be acquired and their total area.

The solution:

Firstly, st_buffer() of sf package is used to compute the 5-meter buffers around cycling paths

buffer_cycling <- st_buffer(cyclingpath, dist = 5, nQuadSegs = 30)

Then, calculate the area of the buffers:

buffer_cycling$AREA <- st_area(buffer_cycling)

Then sum the total area to derive the total land involved.

sum(buffer_cycling$AREA)

1774367 [m^2]

8.2 Point-in-polygon Count

The scenario:

A pre-school service group want to find out the numbers of pre-schools in each Planning Subzone.

The solution:

The code chunk below performs two operations at one go. Firstly, identify pre-schools located inside each Planning Subzone by using st_intersects(). Next, length() of Base R is used to calculate numbers of pre-schools that fall inside each planning subzone.

First, we calculate the number of preschools in each subzone:

mpsz3414$'PreSch Count' <- lengths(st_intersects(mpsz3414, preschool3414))

Then, check the summary statistics of the PreSch count filed using summary():

summary(mpsz3414$'PreSch Count')

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   0.00    0.00    4.00    7.09   10.00   72.00

We use top_n() to list the planning subzone with the most number of pre-school:

top_n(mpsz3414, 1, 'PreSch Count')

Simple feature collection with 323 features and 16 fields
Geometry type: MULTIPOLYGON
Dimension:     XY
Bounding box:  xmin: 2667.538 ymin: 15748.72 xmax: 56396.44 ymax: 50256.33
Projected CRS: SVY21 / Singapore TM
First 10 features:
   OBJECTID SUBZONE_NO       SUBZONE_N SUBZONE_C CA_IND      PLN_AREA_N
1         1          1    MARINA SOUTH    MSSZ01      Y    MARINA SOUTH
2         2          1    PEARL'S HILL    OTSZ01      Y          OUTRAM
3         3          3       BOAT QUAY    SRSZ03      Y SINGAPORE RIVER
4         4          8  HENDERSON HILL    BMSZ08      N     BUKIT MERAH
5         5          3         REDHILL    BMSZ03      N     BUKIT MERAH
6         6          7  ALEXANDRA HILL    BMSZ07      N     BUKIT MERAH
7         7          9   BUKIT HO SWEE    BMSZ09      N     BUKIT MERAH
8         8          2     CLARKE QUAY    SRSZ02      Y SINGAPORE RIVER
9         9         13 PASIR PANJANG 1    QTSZ13      N      QUEENSTOWN
10       10          7       QUEENSWAY    QTSZ07      N      QUEENSTOWN
   PLN_AREA_C       REGION_N REGION_C          INC_CRC FMEL_UPD_D   X_ADDR
1          MS CENTRAL REGION       CR 5ED7EB253F99252E 2014-12-05 31595.84
2          OT CENTRAL REGION       CR 8C7149B9EB32EEFC 2014-12-05 28679.06
3          SR CENTRAL REGION       CR C35FEFF02B13E0E5 2014-12-05 29654.96
4          BM CENTRAL REGION       CR 3775D82C5DDBEFBD 2014-12-05 26782.83
5          BM CENTRAL REGION       CR 85D9ABEF0A40678F 2014-12-05 26201.96
6          BM CENTRAL REGION       CR 9D286521EF5E3B59 2014-12-05 25358.82
7          BM CENTRAL REGION       CR 7839A8577144EFE2 2014-12-05 27680.06
8          SR CENTRAL REGION       CR 48661DC0FBA09F7A 2014-12-05 29253.21
9          QT CENTRAL REGION       CR 1F721290C421BFAB 2014-12-05 22077.34
10         QT CENTRAL REGION       CR 3580D2AFFBEE914C 2014-12-05 24168.31
     Y_ADDR SHAPE_Leng SHAPE_Area                       geometry PreSch Count
1  29220.19   5267.381  1630379.3 MULTIPOLYGON (((31495.56 30...            0
2  29782.05   3506.107   559816.2 MULTIPOLYGON (((29092.28 30...            6
3  29974.66   1740.926   160807.5 MULTIPOLYGON (((29932.33 29...            0
4  29933.77   3313.625   595428.9 MULTIPOLYGON (((27131.28 30...            5
5  30005.70   2825.594   387429.4 MULTIPOLYGON (((26451.03 30...            3
6  29991.38   4428.913  1030378.8 MULTIPOLYGON (((25899.7 297...           13
7  30230.86   3275.312   551732.0 MULTIPOLYGON (((27746.95 30...            5
8  30222.86   2208.619   290184.7 MULTIPOLYGON (((29351.26 29...            1
9  29893.78   6571.323  1084792.3 MULTIPOLYGON (((20996.49 30...           11
10 30104.18   3454.239   631644.3 MULTIPOLYGON (((24472.11 29...            1

To calculate the density of pre-school by planning subzone. we first derives the area of each planning subzone:

mpsz3414$Area <- mpsz3414 %>% 
  st_area()

Then use mutate() to compute the density of preschool by planning subzone

mpsz3414 <- mpsz3414 %>% 
    mutate(`PreSch Density` = `PreSch Count`/Area * 1000000)

9 Exploratory Data Analysis

In this section, we will learn how to use appropriate ggplot2 functions to create statistical graphs for exploratory data analysis purposes.

One quick way to plot the preschool density is to use hist() of R graphics:

hist(mpsz3414$`PreSch Density`)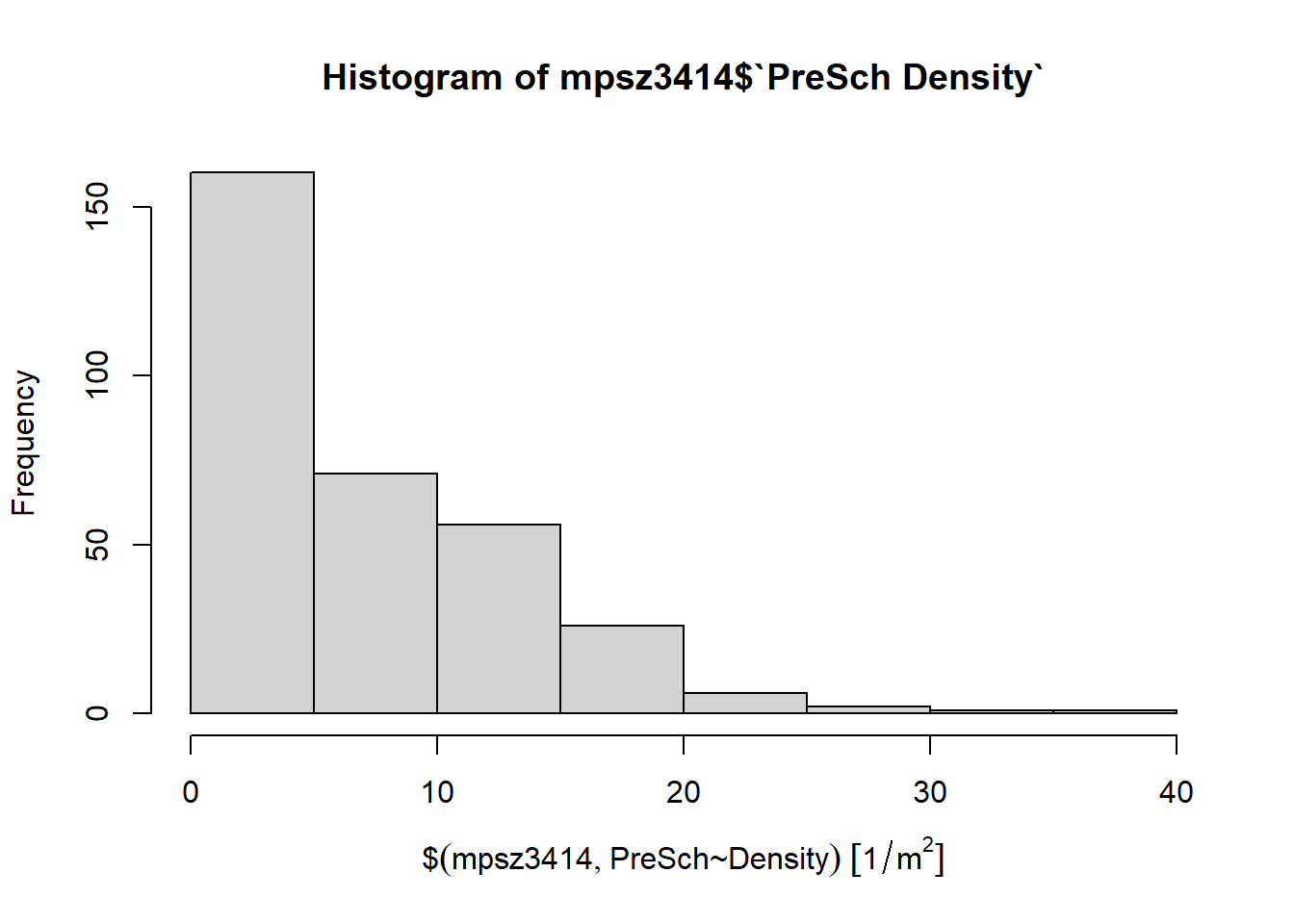

However hist() has limited room for further customisation. Hence, we will use functions from ggplot2:

ggplot(data = mpsz3414,
       aes(x = as.numeric(`PreSch Density`))) + 
  geom_histogram(bins = 20,
                 color = "black",
                fill = "light blue") + 
  labs(title = "Are Pre-Schools Evenly Distributed in Singapore?",
       subtitle = "There are many planning subszones with a single pre-school, on the other hand, \nthere are two planning subszones with at least 20 preschools",
       x = "PreSchool Density (per km sq)",
       y = "Frequency")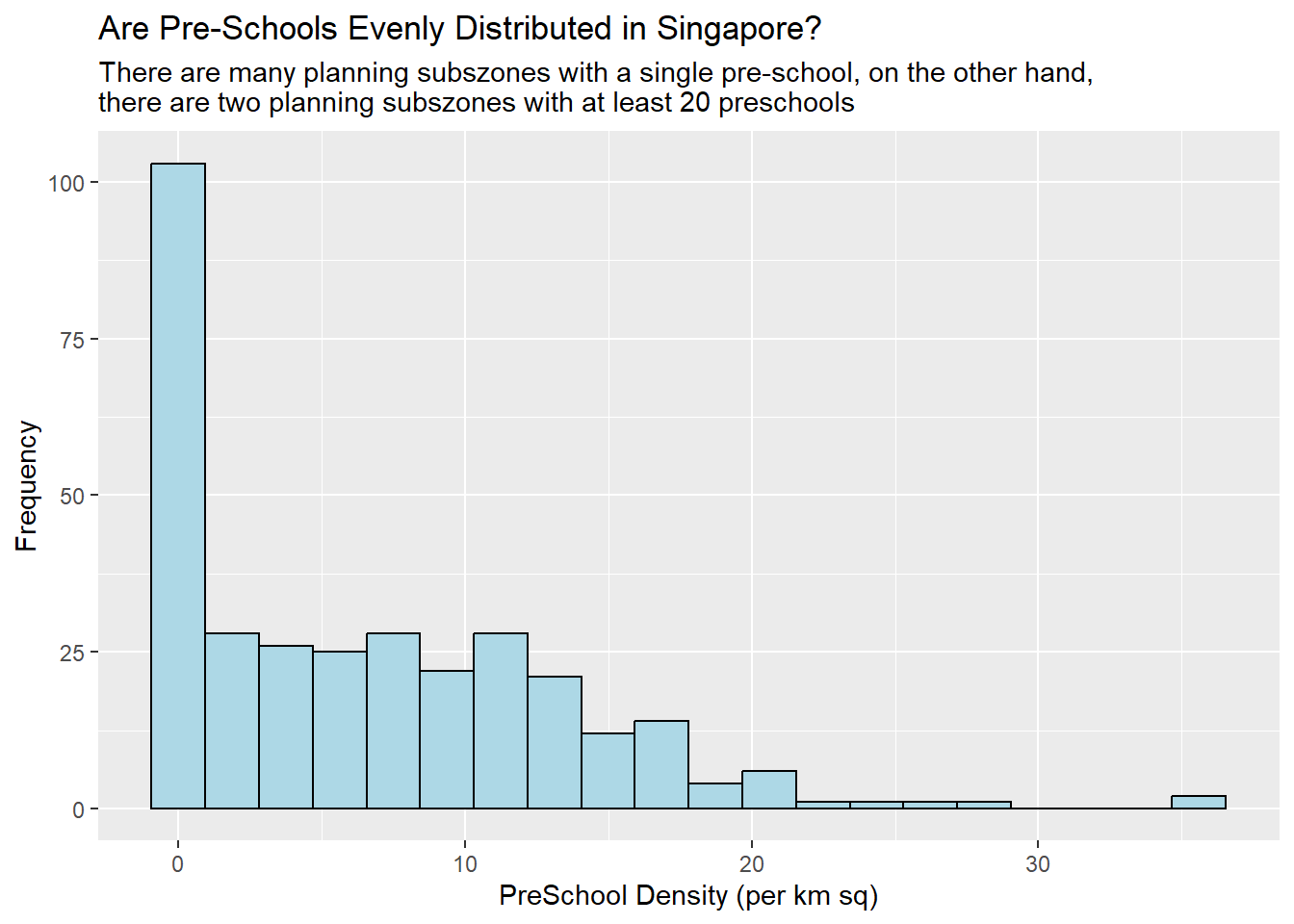

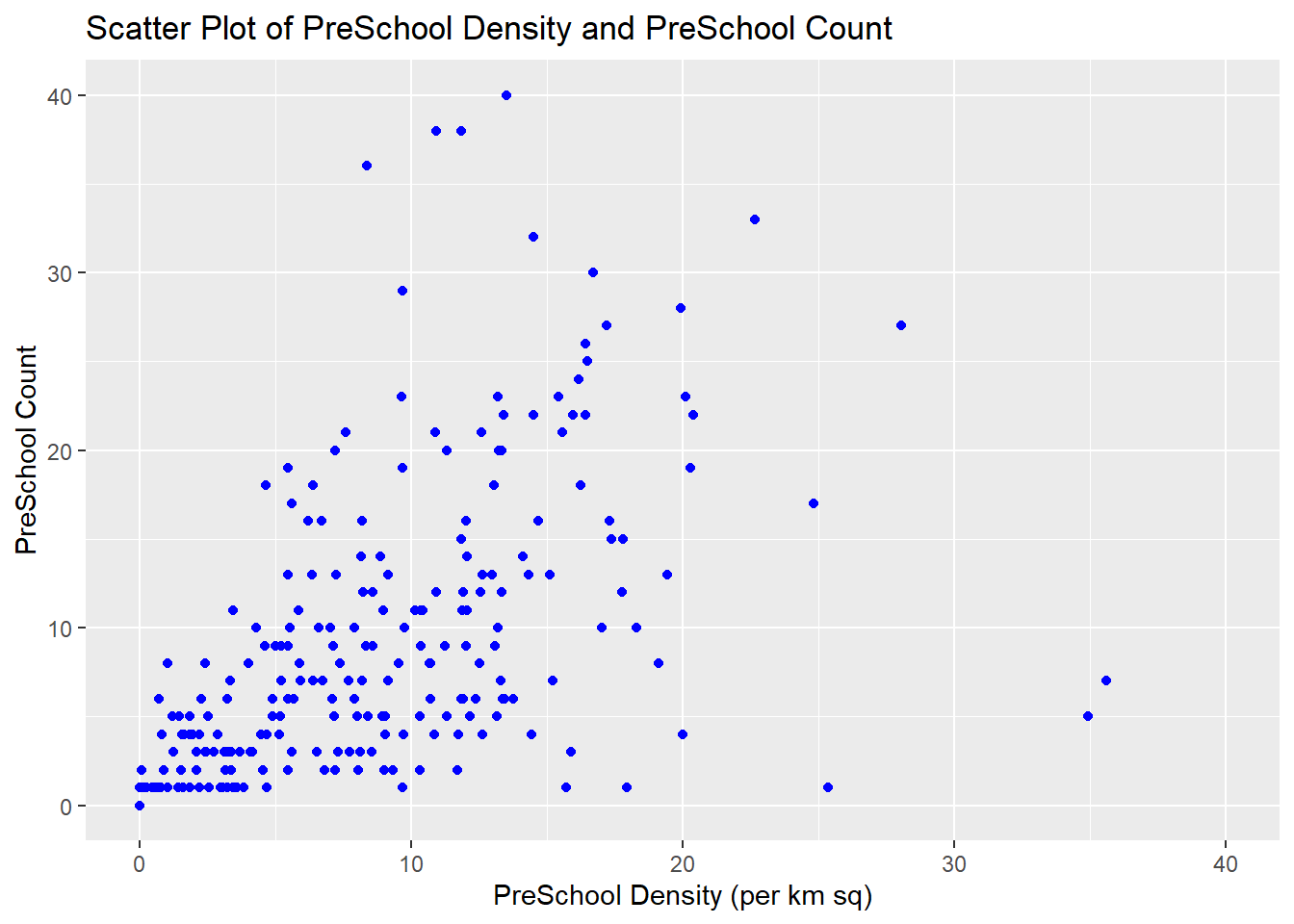
Here is a scatterplot showing the relationship between pre-school density and pre-school count.

ggplot(data = mpsz3414,
       aes(y = `PreSch Count`,
         x = as.numeric(`PreSch Density`))) +
  geom_point(color = "blue") + 
  xlim(0, 40) + 
  ylim(0, 40) + 
  labs(title = "Scatter Plot of PreSchool Density and PreSchool Count", 
       x = "PreSchool Density (per km sq)", 
       y = "PreSchool Count")